Optimizing chunks for matrix multiplication in Blosc2

Matrix Multiplication

Matrix multiplication is a fundamental operation in many scientific and engineering applications. With the introduction of matrix multiplication into Blosc2, users can now perform this operation on compressed arrays efficiently. The key advantages of having matrix multiplication in Blosc2 include:

• Compressed matrices in memory: Blosc2 enables matrices to be stored in a compressed format without sacrificing the ability to perform operations directly on them.

• Efficiency with chunks: In computation-intensive applications, matrix multiplication can be executed without fully decompressing the data, operating on small blocks of data independently, saving both time and memory.

• Out-of-core computation: When matrices are too large to fit in main memory, Blosc2 facilitates out-of-core processing. Data stored on disk is read and processed in optimized chunks, allowing matrix multiplication operations without loading the entire dataset into memory.

These features are especially valuable in big data environments and in scientific or engineering applications where matrix sizes can be overwhelming, enabling complex calculations efficiently.

Implementation

The matrix multiplication functionality is implemented in the matmul function. It supports Blosc2 NDArray objects and leverages chunked operations to perform the multiplication efficiently.

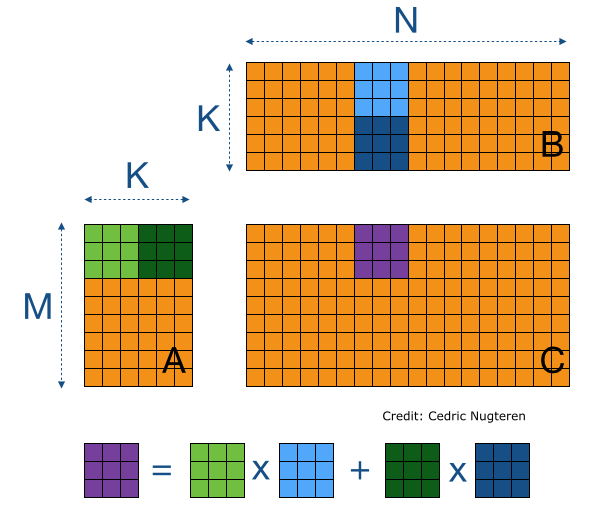
The image illustrates a blocked matrix multiplication approach. The key idea is to divide matrices into smaller blocks (or chunks) to optimize memory access and computational efficiency.

In the image, matrix A (M x K) and matrix B (K x N) are partitioned into chunks, and these are partitioned into blocks. The resulting matrix C (M x N) is computed as a sum of block-wise multiplication.

This method significantly improves cache utilization by ensuring that only the necessary parts of the matrices are loaded into memory at any given time. In Blosc2, storing matrix blocks as compressed chunks reduces memory footprint and enhances performance by enabling on-the-fly decompression.

Also, Blosc2 supports a wide range of data types. In addition to standard Python types such as int, float, and complex, it also fully supports various NumPy types. The currently supported types include:

• np.int8

• np.int16

• np.int32

• np.int64

• np.float32

• np.float64

• np.complex64

• np.complex128

This versatility allows compression and subsequent processing to be applied across diverse scenarios, tailored to the specific needs of each application.

Together, these features make Blosc2 a flexible and adaptable tool for various scenarios, but especially suited for the handling of large datasets.

Benchmarks

The benchmarks have been designed to evaluate the performance of the matmul function under various conditions. Here are the key aspects of our experimental setup and findings:

Different matrix sizes were tested using both float32 and float64 data types. All the matrices used for multiplication are square. The variation in matrix sizes helps observe how the function scales and how the overhead of chunk management impacts performance.

The x-axis represents the size of the resulting matrix in megabytes (MB). We used GFLOPS (Giga Floating-Point Operations per Second) to gauge the computational throughput, allowing us to compare the efficiency of the matmul function relative to highly optimized libraries like NumPy.

Blosc2 also incorporates a functionality to automatically select chunks, and it is represented in the benchmark by "Auto".

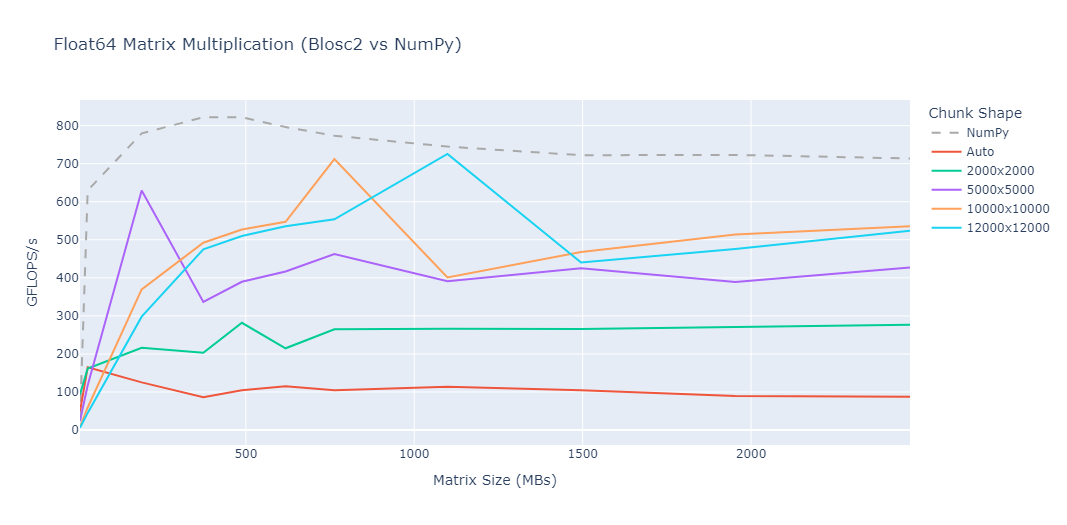
For smaller matrices, the overhead of managing chunks in Blosc2 can result in lower GFLOPS compared to NumPy. As the matrix size increases, Blosc2 scales well, approaching its performance to NumPy.

Each chunk shape exhibits a peak performance when the matrix size matches the chunk size, or is a multiple of the chunk shape.

Conclusion

The new matrix multiplication feature in Blosc2 introduces efficient, chunked computation for compressed arrays. This allows users to handle large datasets both in memory and on disk without sacrificing performance. The implementation supports a wide range of data types, making it versatile for various numerical applications.

Real-world applications, such as neural network training, demonstrate the potential benefits in scenarios where memory constraints and large data sizes are common. While there are some limitations —such as support only for 2D arrays and the overhead of blocking— the applicability looks promising, like potential integration with deep learning frameworks.

Overall, Blosc2 offers a compelling alternative for applications where the advantages of compression and out-of-core computation are critical, paving the way for more efficient processing of massive datasets.

Getting my feet wet with Blosc2

In the initial phase of the project, my biggest challenge was understanding how Blosc2 manages data internally. For matrix multiplication, it was critical to grasp how to choose the right chunks, since the operation requires that the ranges of both matrices coincide. After some considerations and a few insightful conversations with Francesc, I finally understood the underlying mechanics. This breakthrough allowed me to begin implementing the first versions of my solution, adjusting the data fragmentation so that each block was properly aligned for precise computation.

Another important aspect was adapting to the professional workflow of using Git for version control. Embracing Git —with its branch creation, regular commits, and conflict resolution— represented a significant shift in my development approach. This experience not only improved the organization of my code and facilitated collaboration but also instilled a structured and disciplined mindset in managing my projects. This tool has shown to be both valuable and extremely helpful.

Finally, the moment when the function finally returned the correct result was really exciting. After multiple iterations, the rigorous debugging process paid off as everything fell into place. This breakthrough validated the robustness of the implementation and boosted my confidence to further optimize and tackle new challenges in data processing.